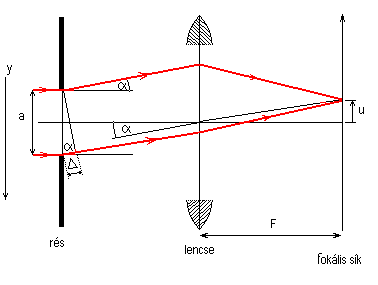
1.Fraunhofer elhajlás (diffrakció) résen

Az egyszerűség kedvéért egy keskeny, szélességénél jóval hosszabb, így gyakorlatilag végtelen hosszúnak tekinthető rést vizsgálunk, melynek síkjára merőlegesen párhuzamos sugárnyaláb esik. Az eredeti iránnyal a szöget bezáró irányban haladó szélső sugarak között az útkülönbség:

A fáziskülönbség:

Ám D==a sin a, így

A közbenső sugarak fázisa egyenletesen nő nullától a Df értékig a

törvény szerint.

A rés minden pontjából másodlagos hullámok indulnak ki az a irányba, és ezek interferálnak. Az eredő hullámot a komplex amplitúdók összegezésével kapjuk meg. Mivel a résben végtelensok pontból indulnak a másodlagos hullámok, integrálunk az y irány mentén a rés teljes szélességén. Így az a irányban észlelt eredő komplex amplitúdó

E = E[0]*int(exp(-2*i*Pi*y*sin*alpha/lambda),y = 0 ...

Felhasználjuk az Euler-féle formulát, nevezetesen az e^ix=cos x +i sin x azonosságot, a továbbá azt, hogy az intenzitás= E.E_konjugált a következő összefüggést kapjuk:

I = I[0]*(int(sin(2*Pi*y*sin(alpha)/lambda),y = 0 ....

Ezután kiszámítva az integrálokat:

I = a^2*I[0]*(sin(Delta*phi/2)/(Delta*phi/2))^2

ahol a Df a fenti jelentéssel bír. Namost: az a szög lévén kicsi, amennyiben csak 2-3° értékű vagy ennél kisebb, sin a = tg a jó közelítéssel, ezért sin a= u/F(lásd az ábrát). Ez az összefüggés a fény intenzitáseloszlását adja meg, a maximális intenzitást egységnyinek véve, a vízszintes tengelyen a fokális síkban felfele mutató u tengelyt adtuk itt meg. Ez kb így néz ki:

[Maple Plot]

Ugyanez, szemből nézve (monokromatikus fényre, nem pedig fehér fényre!):

[Maple Plot]

Fehér fény esetén az oldalsó maximumok kicsit a hullámhossztól függően más-más helyen keletkeznek, ezért az oldalsó maximumok színesek. Megemlítem, hogy az itt látható ábrát egy kissé "túlexponáltam", mert az elsőrendű maximum a középsőnek csupán 4,72 %-a, a másodrendű pedig csupán 1,65 %-a, a többi csak erős fényben látszik. Érdekes módon az emberi szem ezeket is érzékeli, ami sokat elárul a szemünk érzékenységéről.